Module programmation: le langage CAML.

Partie: I
Présentation détaillée du langage

La programmation fonctionnelle

Expressions et valeurs

types de base
- int (entiers relatifs: 3, -4; opérateurs: +, -, *, /, mod, ...)
- float (flottants: 0.5, 3.4E4, 4.3e-2; opérateurs: +., -., *., /., exp, log, sin, ...)
- bool (valeurs de vérité: true, false; opérateurs: && (« et »), || (« ou »), not (« non »); opérateurs de comparaison <, <=, >, >= produisent des résultats booléens et s'appliquent sur des entiers ou des flottants; opérateur d'égalité =)
- string (chaîne de caractères, portion de texte encadrée par des guillemets: "salut les copains", ""; opérations: ^ (concaténation, mise bout à bout de deux chaînes), etc.)

déclarations globales

On parle de déclaration, définition ou de liaison.

let ident = expression;;

#let s = 1 + 2 + 3;;
s : int = 6
#let s_carré = s * s;;
s_carré : int = 36

#s_carré;;
- : int = 36
#s_carré - rintintin;;
Entrée interactive:
>s_carré - rintintin;;
>          ^^^^^^^^^
L'identificateur rintintin n'est pas 
défini.
#let s = 3 * 3;;
s : int = 9
#s_carré;;
- : int = 36
#let s = "pourquoi pas une chaîne";;
s : string = "pourquoi pas une chaîne"
#s^"!!!";;
- : string = "pourquoi pas une chaîne!!!"

déclarations locales

let ident = expr1 in expr2;;

#let x = 5 * 5 in x + 2;;
- : int = 27
#x;;
Entrée interactive:
>x;;
>^
L'identificateur x n'est pas défini.
#let x = 3;;
x : int = 3
#let x = 5 * 5 in x + 2;;
- : int = 27
#x;;
- : int = 3
#(2*3+6) * (2*3+6) + 2 * (2*3+6) + 5;;
- : int = 173
#let a = 2*3+6 in a * a + 2 * a + 5;;
- : int = 173
#let z=3 in 
   let t=z+1 in z+t+1;;
- : int = 8

déclarations simultanées

globales

let ident1 = expr1
and ident2 = expr2;;

ou locales

let ident1 = expr1
and ident2 = expr2 in
expr;;

#let x = 1;;
x : int = 1
#let x = x+1 and y = x;;
x : int = 2
y : int = 1

expressions conditionnelles

if condition then expression1 else expression2
utilisation des parenthèses (priorités des opérateurs, levée d'ambiguité)

Modules et importation en bref

#sys__getenv;;
- : string -> string = <fun>
#getenv;;
Entrée interactive:
>getenv;;
>^^^^^^
L'identificateur getenv n'est pas défini.

Voir les noms exportés par sys

##open "sys";;
#getenv;;
- : string -> string = <fun>
#getenv "DISPLAY";;
- : string = ":0.0"
#getenv "PRINTER";;
Exception non rattrapée: Not_found

Cacher les noms exportés par sys

##close "sys";;
#getenv;; 
Entrée interactive:
>getenv;; 
>^^^^^^
L'identificateur getenv n'est pas défini.

Les différents types de bibliothèques

La core library: modules importés par défaut. Par exemple, le module string

#string_length;;
- : string -> int = <fun>
##close "string";;
#string_length;;
Entrée interactive:
>string_length;;
>^^^^^^^^^^^^^
L'identificateur string_length n'est pas 
défini.
##open "string";;

La standard library: modules à importer. Par exemple, le module sys ou random:

#random__init;;
- : int -> unit = <fun>
#random__int;;
- : int -> int = <fun>
##open "random";;
#init;;
- : int -> unit = <fun>

Les autres bibliothèques (graphics, unix, num, str): modules à importer dans un toplevel spécial pour que ces modules soient linkés avec le reste de Caml. Par exemple pour la bibliothèque graphique :

Unix: $ camllight camlgraph
>       Caml Light version 0.74

##open "graphics";;
#open_graph "";;     
- : unit = ()
#draw_circle 200 200 50;;   
- : unit = ()
#close_graph ();;
- : unit = ()
##close "graphics";;
#open_graph "";;     
Entrée interactive:
>open_graph "";;     
>^^^^^^^^^^
L'identificateur open_graph n'est pas défini.

à comparer avec

Unix: $ camllight
>       Caml Light version 0.74

##open "graphics";;
#open_graph "";;     
La valeur globale graphics__open_graph est 
utilisée avant d'être définie.
Veuillez charger une implémentation du 
module graphics.

Fonctions

fonction d'une variable, définition, application

anonyme

  function paramètre -> 
  expression_du_corps_de_la_fonction;;

#function a -> if a < 0 then -a else a;;
- : int -> int = <fun>

nommée

let nom_de_la_fonction = 
  function paramètre ->
  expression_du_corps_de_la_fonction;;

let nom_de_la_fonction paramètre = 
  expression_du_corps_de_la_fonction;;

#let abs = function a -> 
   if a < 0 then -a else a;;
abs : int -> int = <fun>
#let abs a = if a < 0 then -a else a;;
abs : int -> int = <fun>
#let carré = function x -> x * x;;
carré : int -> int = <fun>

#let polynôme = function x ->
   let a = 2 
   and b = -3 
   and c = 5 in a * x * x + b * x + c;;
polynôme : int -> int = <fun>
#let répéter = function s -> s ^ s;;
répéter : string -> string = <fun>
#let est_vide = function s -> s = "";;
est_vide : string -> bool = <fun>

appliquée

#carré 5;;
- : int = 25
#carré(5);;
- : int = 25
#carré (4 - 5);;
- : int = 1
#carré 4 - 5;; 
- : int = 11
#répéter "cou";;
- : string = "coucou"

fonctions à plusieurs arguments

let nom_de_la_fonction p1 ... pn = 
  expression_du_corps_de_la_fonction;;
let nom_de_la_fonction = 
  function p1 -> ... -> function pn -> 
  expression_du_corps_de_la_fonction;;

#let surface_rectangle long large = 
   long *. large;;
surface_rectangle : float -> float -> 
float = <fun>
#let surface_rectangle = 
   function long -> 
     function large -> long *. large;;
surface_rectangle : float -> float -> 
float = <fun>
#surface_rectangle 1.4 2.4;;
- : float = 3.36

portée statique

#let const=3;;
const : int = 3
#let f = function x -> x*const;;
f : int -> int = <fun>
#f 1;;
- : int = 3
#let const=6;;
const : int = 6
#f 1;;
- : int = 3

type d'une fonction (t1 -> t2)

function x -> expr est de type t1 -> t2, si t1 est le type du paramètre formel x et t2 le type de l'expression expr

#let identité = function x -> x;;
identité : 'a -> 'a = <fun>
#identité 3;;
- : int = 3
#identité true;;
- : bool = true
#identité "une chaîne";;
- : string = "une chaîne"

identité est une fonction polymorphe.

restriction du domaine de définition d'une fonction

failwith "message d'erreur"

#let H = function x ->
   if x = 1 then failwith "H: indéfini" 
   else 1 / (x - 1);;
H : int -> int = <fun>
#let prédécesseur = function y ->
   if y <= 0 
   then failwith "paramètre non naturel" 
   else y - 1;; 
prédécesseur : int -> int = <fun>
#H 5;;
- : int = 0
#H 1;;
Exception non rattrapée: Failure "H: 
indéfini"
#prédécesseur 2;;
- : int = 1

#prédécesseur (-5);;
Exception non rattrapée: Failure 
"paramètre non naturel"
#carré (H (3-abs(2)));;
Exception non rattrapée: Failure "H: 
indéfini"
#failwith;;
- : string -> 'a = <fun>

Il existe aussi le mot-clé fun qui est équivalent à function dans les cas simples (un seul argument, etc.), mais diffère subtilement par ailleurs avec une sémantique plus floue. fun ne sera pas utilisé dans ce cours.

Fonctions récursives

syntaxe: let rec

exemples classiques: factorielle, suite de Fibonacci, pgcd d'entiers

#let fact = function n ->
   if n <= 0 then 1 else n*fact(n-1);;
Entrée interactive:
>  if n <= 0 then 1 else n*fact(n-1);;
>                          ^^^^
L'identificateur fact n'est pas défini.
#let rec fact = function n -> 
   if n <= 0 then 1 else n*fact(n-1);;
fact : int -> int = <fun>
#let rec fib = function n -> 
   if n <= 1 then 1 
   else fib (n-1)+fib(n-2);;
fib : int -> int = <fun>
#let rec pgcd = function a -> function b ->
   if b = 0 then abs a 
   else pgcd b (a mod b);;
pgcd : int -> int -> int = <fun>

un exemple de fonctions mutuellement récursives: pair et impair

#let rec pair = function n ->
   if n=0 then true else impair (n-1)
 and impair = function n ->
   if n=0 then false else pair (n-1);;
pair : int -> bool = <fun>
impair : int -> bool = <fun>
#impair 10;;
- : bool = false
#pair 10;;
- : bool = true
#impair 11;;
- : bool = true
#pair 11;;
- : bool = false

définition d'une fonction récursive:
- un ou plusieurs cas de base (calcul direct du résultat sans rappeler la fonction)
- cas récursifs qui se rapprochent à chaque itération des cas de base

Listes (début du filtrage)

un type de données prédéfini, qui n'utilise pas de pointeurs, avec une importante bibliothèque de fonctions prédéfinies!
Une liste est une suite (ordonnée) de valeurs de même nature de longueur non prédéfinie.
Syntaxe ([],[v1;...;vn])

Type : une liste de valeurs de type t est de type t list.

#[1; 2; 3];;
- : int list = [1; 2; 3]
#[true; 1 < 2];;
- : bool list = [true; true]
#[(function x -> x+2); succ; abs];;
- : (int -> int) list = [<fun>; <fun>; 
<fun>]
#[1; 2; "trois"];;
Entrée interactive:
>[1; 2; "trois"];;
>^^^^^^^^^^^^^^^
Cette expression est de type string list,
mais est utilisée avec le type int list.

#[[1; 2]; [2; 3; 4]; [9]];;
- : int list list = [[1; 2]; [2; 3; 4]; 
[9]]

La liste vide pourra être considérée comme une liste d'entiers, une liste de chaînes, une liste d'objets de type t pour tout type t selon le contexte d'utilisation.

#if (1>2) then [1] else [];;
- : int list = []
#[["a"; "b"]; []; ["c"]] ;;
- : string list list = [["a"; "b"]; []; 
["c"]]
#[];;
- : 'a list = []

L'opérateur ::

L'opérateur prédéfini noté :: se lit souvent cons (prononcer le s final). Il s'agit d'un opérateur infixe permettant de construire une nouvelle liste à partir d'une liste l et d'un élément x. L'expression x::l dénote la liste composée de l'élément x puis des éléments de l. Si l est de type t list, x doit être de type t.
```
#1::[2];;
- : int list = [1; 2]
#true::[2];;
Entrée interactive:
>true::[2];;
>      ^^^
Cette expression est de type int list,
mais est utilisée avec le type bool list.
#1::(2::(3::[]));;
- : int list = [1; 2; 3]
```

Fonctions simples manipulant des listes

La fonction tête « si la liste l est vide alors le calcul échoue en affichant la chaîne de caractères "tête: liste vide", si la liste n'est pas vide alors appelons x son premier élément et l' la liste de ses autres éléments, la valeur de l'expression est alors x ».
```
#let tête = function l -> 
 match l with
 | [] -> failwith "tête: liste vide"
 | x::l' -> x;;
tête : 'a list -> 'a = <fun>
#tête [];;
Exception non rattrapée: Failure "tête: 
liste vide"
#tête [1; 2; 3];;
- : int = 1
```
La fonction tête est disponible en Caml sous le nom hd.

La fonction reste

#let reste = function l ->
 match l with
 | [] -> failwith "reste: liste vide"
 | x::l' -> l';;
reste : 'a list -> 'a list = <fun>
#let reste = function l ->
 match l with
 | [] -> failwith "reste: liste vide"
 | _::l' -> l';;
reste : 'a list -> 'a list = <fun>
#reste [];;
Exception non rattrapée: Failure "reste: 
liste vide"
#reste [1; 2; 3];;
- : int list = [2; 3]

La fonction reste est disponible en Caml sous le nom tl.

La fonction zéro_en_tête

#let zéro_en_tête = function l ->
 match l with 
 | [] -> false
 | x::l' -> x=0;;
zéro_en_tête : int list -> bool = <fun>
#let zéro_en_tête = function l ->
 match l with
 | 0::_ -> true
 | _ -> false;;
zéro_en_tête : int list -> bool = <fun>
#zéro_en_tête [];;
- : bool = false
#zéro_en_tête [1; 2; 3];;
- : bool = false
#zéro_en_tête [0; 1; 2; 3];;
- : bool = true

#let zéro_en_tête = function l ->
 match l with
 | _ -> false
 | 0::_ -> true;;
Entrée interactive:
>| 0::_ -> true;;
>  ^^^^
Attention: ce cas de filtrage est 
inutile.
zéro_en_tête : int list -> bool = <fun>
#zéro_en_tête [0; 1; 2; 3];;
- : bool = false

La fonction élément2

#let élément2 = function l ->
 match l with 
 | x1::x2::l' -> x2
 | _ -> failwith "élément2: |liste| < 2";;
élément2 : 'a list -> 'a = <fun>
#let élément2 = function l ->
 match l with
 | _::x2::_ -> x2
 | _ -> failwith "élément2: |liste| < 2";;
élément2 : 'a list -> 'a = <fun>

#élément2 [];;
Exception non rattrapée: Failure 
"élément2: |liste| < 2"
#élément2 [1];;
Exception non rattrapée: Failure 
"élément2: |liste| < 2"
#élément2 [1;2;3];;
- : int = 2
#let élément2 = function l ->
 tête (reste l);;
élément2 : 'a list -> 'a = <fun>
#élément2 [];;
Exception non rattrapée: Failure "reste: 
liste vide"
#élément2 [1];;
Exception non rattrapée: Failure "tête: 
liste vide"
#élément2 [1;2;3];;
- : int = 2

Filtrage

On appelle filtrage ou analyse de cas une expression qui décrit un calcul selon la forme que prend une autre expression.

On appelle filtre ou motif la description de la forme attendue. Dans les exemples précédents, il s'agit par exemple de [], x::l, _, x::_, x1::x2::_. Le filtre permet non seulement de préciser la forme attendue mais aussi d'extraire et de nommer certaines parties d'une valeur.

Un filtrage apparaît comme une suite de cas tous composés d'un filtre et d'une expression. Chaque cas est syntaxiquement noté

| filtre -> expression. Le premier « | » peut être omis. Donc un filtrage prend la forme syntaxique générale suivante

match exp with
| filtre₁ -> exp₁
...
| filtre_n -> exp_n

où exp, exp₁, ..., exp_n sont des expressions et filtre₁, ..., filtre_n sont des filtres.

exp₁, ..., exp_n doivent toutes avoir le même type et filtre₁, ..., filtre_n doivent tous être des filtres du type de exp. Il faut que tous les filtres recouvrent tous les cas possibles.

#let tête_imparfaite = function l ->
 match l with
 | x::_ -> x;;
Entrée interactive:
>match l with
>| x::_ -> x..
Attention: ce filtrage n'est pas 
exhaustif.
tête_imparfaite : 'a list -> 'a = <fun>
#tête_imparfaite [1;2;3];;
- : int = 1
#tête_imparfaite [];;
Exception non rattrapée: Match_failure 
("", 3349, 3373)

Récapitulatif des filtres de listes

Dans la composition d'un filtre de listes, il peut entrer :

Les constantes (par exemple 0)
Les identificateurs (par exemple x ou l dans les fonctions sur les listes)
Le signe _ comme cas par défaut ou pour éviter de nommer un identificateur qui n'apparaît pas dans le corps de ce cas
La liste vide []
Et enfin un filtre défini par le constructeur :: avec un élément que l'on peut lui-même filtrer et une liste que l'on peut filtrer elle aussi (filtre::filtre).

Attention, si l'identificateur x est défini, le filtre x::_ ne filtre pas les listes commençant par x, mais toutes les listes en nommant x son premier élément indépendamment de l'identificateur x préexistant et dans l'expression associée au filtre x correspond au premier élément de la liste filtrée. Si on veut filtrer les listes commençant par x, alors il faut écrire y::_ when y=x. Le when condition s'appelle la garde du filtre.

Fonctions récursives manipulant des listes

Longueur d'une liste

#let rec length = function l ->
 match l with
 | [] -> 0
 | _::l' -> 1+(length l');;
length : 'a list -> int = <fun>
#length [1; 2; 3];;
- : int = 3

La fonction length est prédéfinie comme list_length.

Recherche d'un élément dans une liste

#let rec member = function e -> function l ->
 match l with
 | [] -> false
 | x::l' -> 
   if e=x then true else member e l';;
member : 'a -> 'a list -> bool = <fun>
#let rec member = function e -> function l ->
 match l with
 | [] -> false
 | x::l' -> e=x || (member e l');;
member : 'a -> 'a list -> bool = <fun>

#let rec member = function e -> function l ->
 match l with
 | [] -> false
 | x::_ when x=e -> true 
 | _::l' -> member e l';;
member : 'a -> 'a list -> bool = <fun>
#member 0 [1; 2; 3];;
- : bool = false
#member 2 [1; 2; 3];;
- : bool = true
#member 2 [3; 2; 1];;
- : bool = true

La fonction member est prédéfinie sous le nom de mem en Caml.

Recherche d'un élément dans une liste ordonnée

#let rec member_sort = 
   function e -> function l ->
 match l with
 | [] -> false
 | x::l' -> 
   e=x || (x<e && (member_sort e l'));;
member_sort : 'a -> 'a list -> bool = 
<fun>

#let rec member_sort = 
   function e -> function l ->
 match l with
 | [] -> false
 | x::_ when x=e -> true
 | x::_ when x>e -> false
 | _::l' -> member_sort e l';;
member_sort : 'a -> 'a list -> bool = 
<fun>
#member_sort 0 [1; 2; 3];;
- : bool = false
#member_sort 2 [1; 2; 3];;
- : bool = true
#member_sort 2 [3; 2; 1];;
- : bool = false

Dernier élément d'une liste

#let rec dernier = function l ->
 match l with
 | [] -> failwith "dernier: liste vide"
 | [x] -> x
 | _::l' -> dernier l';;
dernier : 'a list -> 'a = <fun>

#dernier [3; 2; 4; 5; 1];;
- : int = 1

Plus grand élément d'une liste

#let rec max_list = function l ->
 match l with
 | [] -> failwith "max_list: liste vide"
 | [x] -> x
 | x::l' -> max x (max_list l');;
max_list : 'a list -> 'a = <fun>
#max_list [3; 2; 4; 5; 1];;
- : int = 5

Fonctions récursives produisant des listes

Liste des entiers compris entre deux bornes

On suppose que i < j et on écrit la liste des entiers compris entre i et j. Cette liste se décompose ainsi


[i; i+1; ...; j] º i::[i+1; ...; j]

#let rec intervalle = 
   function i -> function j ->
     if i = j then [i] 
     else i::(intervalle (i+1) j);;
intervalle : int -> int -> int list = 
<fun>
#intervalle 1 10;;
- : int list = [1; 2; 3; 4; 5; 6; 7; 8; 9; 
10]

Sous-liste des éléments pairs d'une liste

#let rec termes_pairs = function l ->
 match l with
 | [] -> []
 | x::l' ->  
   if x mod 2 = 0 then x::(termes_pairs l') 
   else (termes_pairs l');;
termes_pairs : int list -> int list = 
<fun>
#let rec termes_pairs = function l ->
 match l with
 | [] -> []
 | x::l' when x mod 2 = 0 -> 
   x::(termes_pairs l') 
 | _::l' -> (termes_pairs l');;
termes_pairs : int list -> int list = 
<fun>
#termes_pairs [1; 2; 3; 4; 5];;
- : int list = [2; 4]

Remplacement d'un élément d'une liste par un autre

#let rec remplace = function avant -> 
   function après -> function l ->
 match l with
 | [] -> []
 | x::l' -> 
   if x = avant 
      then après::(remplace avant après l') 
   else x::(remplace avant après l');;
remplace : 'a -> 'a -> 'a list -> 'a list 
= <fun>
#let rec remplace = function avant -> 
   function après -> function l ->
 match l with
 | [] -> []
 | x::l' when x=avant -> 
   après::(remplace avant après l') 
 | x::l' -> x::(remplace avant après l');;
remplace : 'a -> 'a -> 'a list -> 'a list 
= <fun>
#remplace 1 (-1) [1; 2; 1; 4; 100];;
- : int list = [-1; 2; -1; 4; 100]

Concaténation de deux lists, la fonction append

#let rec append = 
   function l1 -> function l2 -> 
 match l1 with
 | [] -> l2
 | x::l'1 -> x::(append l'1 l2);; 
append : 'a list -> 'a list -> 'a list = 
<fun>
#append ["a"; "b"; "c"] ["d"; "ef"];;
- : string list = ["a"; "b"; "c"; "d"; 
"ef"]
#append [1; 2; 3] [];;
- : int list = [1; 2; 3]
#let l = [3; 4];;
l : int list = [3; 4]
#append l l;;
- : int list = [3; 4; 3; 4]
#l;;
- : int list = [3; 4]

Cette fonction est prédéfinie dans le système : (append l1 l2) s'écrit l1 @ l2 en utilisant la primitive de Caml Light.

Types produits

une représentation simple des données composées:
- une date est décrite par un jour, un mois et une année
- un rationnel se compose d'un numérateur et d'un dénominateur...
- on veut les représenter comme un tout (addition de deux rationnels, etc.)
- élément d'un produit cartésien

syntaxe et type: (x₁,x₂,...,x_n) est de type t₁*t₂*...*t_n où t_i est le type de x_i.

#let paire1 = (1, "toto");;
paire1 : int * string = 1, "toto"
#let paire2 = (succ, "une fonction");;
paire2 : (int -> int) * string = <fun>, 
"une fonction"
#(succ 5, let s = "ab" in s ^" "^s);;      
- : int * string = 6, "ab ab"

paramètres ou résultat de fonctions

#let axe_des_x = function n -> (n, 0.0);;
axe_des_x : 'a -> 'a * float = <fun>
#axe_des_x 1.5;;
- : float * float = 1.5, 0.0

#let carré_norme = function v -> 
 match v with 
   | (x,y) -> x *. x +. y *. y;;
carré_norme : float * float -> float = 
<fun>
#carré_norme (2.0, 3.0);;
- : float = 13.0
#let carré_norme = function (x,y) -> 
   x *. x +. y *. y;;
carré_norme : float * float -> float = 
<fun>
#let PS = 
   function (x,y) -> function (x',y') -> 
   x *. x' +. y *. y';;
PS : float * float -> float * float -> 
float = <fun>
#let proj1 = function (x,y) -> x;;
proj1 : 'a * 'b -> 'a = <fun>
#proj1 (2,3);;
- : int = 2
#proj1 ("toto", true);;
- : string = "toto"

#proj1 ((3,4), 5);;
- : int * int = 3, 4
#proj1 (proj1 ((3,4), 5));;
- : int = 3

Un exemple de fonction récursive retournant une paire

#let rec div = function a -> function b ->
   if b=0 then failwith "diviseur nul" else 
   if a<b then (0,a) else 
   match div (a-b) b with 
   | (q,r) -> (q+1,r);;
div : int -> int -> int * int = <fun>
#let rec div = function a -> function b ->
   if b=0 then failwith "diviseur nul" else 
   if a<b then (0,a) else 
   let (q,r) = div (a-b) b in (q+1,r);;
div : int -> int -> int * int = <fun>

let déstructurant.

Les n-uplets

#let carré_norme = function (x, y, z) ->
   x *. x +. y *. y +. z *. z;;
carré_norme : float * float * float -> 
float = <fun>
#let proj1 (x, y, z) = x;;
proj1 : 'a * 'b * 'c -> 'a = <fun>

fonction à n arguments versus fonction à un argument n-uplet
```
#let min = function n -> function m -> 
   if n < m then n else m;;
min : 'a -> 'a -> 'a = <fun>
#let min = function (n, m) -> 
   if n < m then n else m;;
min : 'a * 'a -> 'a = <fun>
```
- n-uplets plus naturels en mathématiques
- fonction à plusieurs arguments traditionnelle en programmation fonctionnelle
- utilisation de la forme la plus naturelle ou appropriée au problème.

Types enregistrements

les premiers types à déclarer, une syntaxe proche de Pascal et de C

déclaration du type

type nom_du_type = 
  { étiquette_1:type_de_étiquette_1;
    étiquette_2:type_de_étiquette_2;
                 :
    étiquette_n:type_de_étiquette_n
  };;

déclaration d'un élément de ce type

let nom_d_identificateur = 
  { étiquette_1 = valeur_de_étiquette_1;
    étiquette_2 = valeur_de_étiquette_2;
                  :
    étiquette_n = valeur_de_étiquette_n
  };;

Les étiquettes doivent être toutes différentes.

exemple

#type date = 
   {Jour: int; Mois: int; Année: int};;
Le type date est défini.
#let Noël_99 = 
   {Jour=25; Mois=12; Année=1999};;
Noël_99 : date = {Jour = 25; Mois = 12; 
Année = 1999}
#let Noël_99_bis = 
   {Année=1999; Mois=12; Jour=25};;
Noël_99_bis : date = {Jour = 25; Mois = 
12; Année = 1999}
#Noël_99 = Noël_99_bis;;
- : bool = true
#Noël_99.Mois;;
- : int = 12
#let est_Noël = function d ->
   d.Jour = 25 && d.Mois = 12;;
est_Noël : date -> bool = <fun>

avec du filtrage

#let est_Noël = function date -> 
 match date with
   | {Jour=j; Mois=m; Année=a} -> 
       j=25 && m=12;;
est_Noël : date -> bool = <fun>
#let est_Noël = function date -> 
   match date with 
   | {Jour=25; Mois=12; Année=a} -> true
   | _ -> false;;
est_Noël : date -> bool = <fun>
#let est_Noell = function date -> 
   match date with 
   | {Jour=25; Mois=12; _} -> true
   | _ -> false;;
est_Noell : date -> bool = <fun>

Types sommes

une notion nouvelle: comment réunir des choux et des carottes en disant proprement que ce sont tous des légumes !
il s'agit d'union disjointe d'ensembles

déclaration

    type nom_du_type = 
    | Constructeur_1 [oftype_1]
    | Constructeur_2 [oftype_2]
                    :
    | Constructeur_n [oftype_n];;

of type_i optionnel (constructeur constant).

Les constructeurs doivent être tous différents.

exemples

#type saison = 
   Printemps | Été | Automne | Hiver;;
Le type saison est défini.
#type boîte = 
 | Cube of float 
 | Parallélépipède of float*float*float;;
Le type boîte est défini.
#Automne;;
- : saison = Automne

#Cube;;
- : float -> boîte = <fun>
#Cube 2.5;;
- : boîte = Cube 2.5

filtrage

#let est_cube = function b -> 
 match b with
 | Cube c -> true
 | Parallélépipède (p1,p2,p3) -> false;;
est_cube : boîte -> bool = <fun>
#let est_cube = function b -> 
 match b with
 | Cube _ -> true
 | Parallélépipède _ -> false;;
est_cube : boîte -> bool = <fun>
#let est_cube  = function b -> 
 match b with
 | Cube _ -> true
 | _ -> false;;
est_cube : boîte -> bool = <fun>

#let est_printemps = function s -> 
 match s with
 | Printemps -> true
 | Été -> false
 | Automne -> false
 | Hiver -> false;;
est_printemps : saison -> bool = <fun>
#let est_printemps = function s -> 
 match s with
 | Printemps -> true
 | _ -> false;;
est_printemps : saison -> bool = <fun>
#let plus_grande_arête = function b -> 
 match b with
 | Cube c -> c
 | Parallélépipède (p1,p2,p3) -> 
     max (max p1 p2) p3;;
plus_grande_arête : boîte -> float = 
<fun>

Types récursifs

un type est récursif si sa définition contient au moins une occurrence de son nom.
La notion de type récursif apparaît naturellement à la suite du chapitre sur les types sommes car un type récursif se définit à l'aide d'un type somme.

De même que la définition d'une fonction récursive contient au moins un cas non récursif que l'on a appelé cas de base) pour assurer la terminaison, il faut que la définition d'un type récursif contienne au moins un constructeur non récursif.

Par exemple:
```
#type type_vide = C of type_vide;;
Le type type_vide est défini.
```
est une déclaration de type valide en Caml, mais il est impossible de construire aucune valeur de ce type.

exemples

Phrases (listes)

#type phrase = 
 | Point | Phrase of string * phrase;;
Le type phrase est défini.
#let sous_chaîne s i = 
   sub_string s i (string_length s-i);;
sous_chaîne : string -> int -> string = 
<fun>

#let rec char_in_string = 
   function c -> function s -> 
     not (s="") && 
     (c=s.[0] || 
      char_in_string c (sous_chaîne s 1));;
char_in_string : char -> string -> bool = 
<fun>
#let rec search = 
   function c -> function s -> 
     if c=s.[0] then 0 
     else 1+(search c (sous_chaîne s 1));;
search : char -> string -> int = <fun>
#let rec coupe = function s ->
   if char_in_string ` ` s then 
     let i = search ` ` s in
     Phrase (sub_string s 0 i, 
             coupe (sous_chaîne s (i+1)))
   else 
     Phrase (
       sub_string s 0 (string_length s-1), 
       Point);;
coupe : string -> phrase = <fun>

#coupe "Une phrase se découpe en mots.";;
- : phrase =
 Phrase
  ("Une",
   Phrase
    ("phrase",
     Phrase ("se", Phrase ("découpe", 
Phrase ("en", Phrase ("mots", Point))))))

On peut comparer le type phrase au type string list où la liste vide serait dénotée Point.

Arbres binaires de recherche à coefficients entiers

Tous les éléments présents dans le sous-arbre droit sad d'un noeud Noeud(elem, sag, sad) sont supérieurs à elem et tous ceux présents dans le sous-arbre gauche sag sont inférieurs à elem.

#type abr = 
 | Vide 
 | Noeud of int * abr * abr;;
Le type abr est défini.
#let mon_arbre = 
   Noeud (10, 
          Noeud (5, 
                 Noeud (2,Vide, Vide), 
                 Noeud (8, Vide, Vide)),
          Noeud (30, 
                 Vide, 
                 Noeud (40, Vide, Vide)));;
mon_arbre : abr =
 Noeud
  (10, Noeud (5, Noeud (2, Vide, Vide), 
Noeud (8, Vide, Vide)),
   Noeud (30, Vide, Noeud (40, Vide, 
Vide)))

#let rec member = 
   function élém -> function a -> 
 match a with
 | Vide -> false
 | Noeud (e, _, _) when e = élém -> true
 | Noeud (e, sag, _) when élém < e -> 
   member élém sag 
 | Noeud (e, _, sad) -> member élém sad;;
member : int -> abr -> bool = <fun>
#member 2 mon_arbre;;
- : bool = true

Arbres binaires de recherche à coefficients d'un type quelconque

#type 'a abr = 
 | Vide 
 | Noeud of 'a * 'a abr * 'a abr;;
Le type abr est défini.

Définition de type polymorphe : 'a est le paramètre de type et se lit a, alpha.

#let mon_arbre = 
   Noeud (10, 
          Noeud (5, 
                 Noeud (2,Vide, Vide), 
                 Noeud (8, Vide, Vide)),
          Noeud (30, 
                 Vide, 
                 Noeud (40, Vide, Vide)));;
mon_arbre : int abr =
 Noeud
  (10, Noeud (5, Noeud (2, Vide, Vide), 
Noeud (8, Vide, Vide)),
   Noeud (30, Vide, Noeud (40, Vide, 
Vide)))

#let rec member = 
   function élém -> function a -> 
 match a with
 | Vide -> false
 | Noeud (e, _, _) when e = élém -> true
 | Noeud (e, sag, _) when élém < e -> 
   member élém sag 
 | Noeud (e, _, sad) -> member élém sad;;
member : 'a -> 'a abr -> bool = <fun>
#member 2 mon_arbre;;
- : bool = true

Expressions arithmétiques (arbres de syntaxe abstraite)

#type exp = 
 | V of string | C of int 
 | P of exp * exp;;
Le type exp est défini.
#let mon_exp = P (V "x", P (V "y", C 3));;
mon_exp : exp = P (V "x", P (V "y", C 3))
#let rec dériv = 
   function s -> function exp -> 
 match exp with 
 | V nom -> 
   if s = nom then C 1 else C 0
 | C _ -> C 0
 | P (e1, e2) -> 
   P (dériv s e1, dériv s e2);;
dériv : string -> exp -> exp = <fun>
#dériv "x" mon_exp;;
- : exp = P (C 1, P (C 0, C 0))

Un peu d'ordre supérieur

Exemples simples

#let pente_en_0 = function f -> 
   (f(0.01)-.f(0.))/.0.01;;
pente_en_0 : (float -> float) -> float = 
<fun>
#let dérivée f = function x -> 
   (f(x+.0.001)-.f(x))/.0.001;;
dérivée : (float -> float) -> float -> 
float = <fun>
#let compose = 
   function f -> function g -> 
     function x -> g (f x);;
compose : ('a -> 'b) -> ('b -> 'c) -> 'a 
-> 'c = <fun>

Itérateurs

Calcul du n-ème terme d'une suite définie récursivement

ì
í
î

u₀	=	a,
u_n+1	=	f(u_n)

#let rec iter = function n -> 
   function f -> function a ->
     if n = 0 then a else f (iter (n-1) f a);;
iter : int -> ('a -> 'a) -> 'a -> 'a = 
<fun>
#let puissance = function p -> function n -> 
   iter n (function x -> p*x) 1;;
puissance : int -> int -> int = <fun>
#puissance 2 15;;
- : int = 32768

Fonction sigma

#let rec somme = function n ->
   if n = 0 then 0 else n+(somme (n-1));;
somme : int -> int = <fun>
#let rec somme_carrés = function n -> 
   if n = 0 then 0 
   else (n*n)+(somme_carrés (n-1));;
somme_carrés : int -> int = <fun>
#let rec sigma = function f -> function n -> 
   if n = 0 then 0 
   else f (n)+(sigma f (n-1));;
sigma : (int -> int) -> int -> int = 
<fun>
#let somme = function n -> 
   sigma (function n -> n) n;;
somme : int -> int = <fun>
#let somme_carrés = function n -> 
   sigma (function n -> n*n) n;;
somme_carrés : int -> int = <fun>

Fonction map

#let rec noms_étudiants = 
   function liste_étudiants ->
 match liste_étudiants with
 | [] -> []
 | (nom, notes)::l -> 
 nom::(noms_étudiants l);;
noms_étudiants : ('a * 'b) list -> 'a list 
= <fun>
#let rec map = 
   function f -> function liste ->
 match liste with
 | [] -> []
 | x::l -> (f x)::(map f l);;
map : ('a -> 'b) -> 'a list -> 'b list = 
<fun>
#map (function x -> x*x) [1; 2; 3; 4; 5; 6];;
- : int list = [1; 4; 9; 16; 25; 36]
#let noms_étudiants = function l ->
   map (function (nom, note) -> nom) l;;
noms_étudiants : ('a * 'b) list -> 'a list 
= <fun>

Cette fonctionnelle map est prédéfinie en Caml.

Algorithmes paramétrés par un prédicat

Fonction filter

#let rec filter = function p -> function l ->
 match l with
 | [] -> []
 | x::l' -> 
   if (p x) then x::(filter p l') 
   else (filter p l');;
filter : ('a -> bool) -> 'a list -> 'a 
list = <fun>
#let termes_pairs = function l ->
   filter (function x -> (x mod 2 = 0)) l;;
termes_pairs : int list -> int list = 
<fun>
#let est_sur_axe_x = function (x,y) -> y=0.0;;
est_sur_axe_x : 'a * float -> bool = 
<fun>
#let vecteurs_axe_x = function l ->
   filter est_sur_axe_x l;;
vecteurs_axe_x : ('a * float) list -> ('a 
* float) list = <fun>

Insertion, tri

#let rec insérer = 
   function e -> function l ->
 match l with
 | [] -> [e]
 | x::l' -> 
   if e < x then e::l 
   else x::(insérer e l');;
insérer : 'a -> 'a list -> 'a list = 
<fun>
#let rec insérer priorité = 
   function e -> function l ->
 match l with
 | [] -> [e]
 | x::l' -> 
   if priorité x e 
      then x::(insérer priorité e l') 
   else e::l;;
insérer : ('a -> 'a -> bool) -> 'a -> 'a 
list -> 'a list = <fun>
#let insérer_ordre_croissant = 
   function e -> function l ->
     insérer (prefix <) e l;;
insérer_ordre_croissant : 'a -> 'a list -> 
'a list = <fun>
#let insérer_ordre_décroissant = 
   insérer (prefix >);;
insérer_ordre_décroissant : '_a -> '_a 
list -> '_a list = <fun>
#let rec tri_insertion = 
   function priorité -> function liste ->
 match liste with 
 | [] -> [] 
 | e::l -> 
   insérer priorité e 
           (tri_insertion priorité l);;
tri_insertion : ('a -> 'a -> bool) -> 'a 
list -> 'a list = <fun>
#let tri_insertion_ordre_croissant = 
   function l -> tri_insertion (prefix <) l;;
tri_insertion_ordre_croissant : 'a list -> 
'a list = <fun>

La programmation impérative

Références

modélisation de la notion de case mémoire: on peut consulter son contenu courant et modifier son contenu.
correspond presque à la notion d'identificateur dans les langages impératifs classiques, Pascal par exemple.
utilisées comme des compteurs ou des accumulateurs dont le contenu évolue au cours du calcul.

Création et type

#let compteur = ref (0);;
compteur : int ref = ref 0

Consultation du contenu courant (déréférencement)

#!compteur;;
- : int = 0

Modification du contenu (affectation, effet de bord)

#compteur:=2;;
- : unit = ()
#!compteur;;
- : int = 2

Exemple de fonction manipulant des références :

#let incrémente = function c -> c := !c+1;;
incrémente : int ref -> unit = <fun>
#incrémente compteur; !compteur;;
- : int = 3

Attention, l'affectation d'une référence est différente de la redéfinition par un let d'un identificateur Caml :

#let x = 1;;

x : int = 1

#let f = function y -> x+y;;

f : int -> int = <fun>

#let x = 2;;

x : int = 2

#f (0);;

- : int = 1

#let x = ref 1;;

x : int ref = ref 1

#let f = function y -> !x+y;;

f : int -> int = <fun>

#x := 2;;

- : unit = ()

#f (0);;

- : int = 2

Tableaux

Tableaux à une dimension (vecteurs)

Figure 0.1 : Les principales notions sur les vecteurs

Création et type

#[|1; 2; 3|];;
- : int vect = [|1; 2; 3|]
#make_vect 4 2;;
- : int vect = [|2; 2; 2; 2|]
#let r = make_vect 3 "Bonjour";;
r : string vect = [|"Bonjour"; "Bonjour"; 
"Bonjour"|]
#let r2 = init_vect 3 (function i -> i*i);;
r2 : int vect = [|0; 1; 4|]

Consultation du contenu courant

#r;;
- : string vect = [|"Bonjour"; "Bonjour"; 
"Bonjour"|]
#r.(0);;
- : string = "Bonjour"

Modification du contenu

#r.(1) <- "tout"; r.(2) <- "le monde!";;
- : unit = ()
#r;;
- : string vect = [|"Bonjour"; "tout"; "le 
monde!"|]

Tableaux à deux dimensions (matrices)

Création, types et dimensions

#[|[|1; 2; 3|]; [|4; 5; 6|]; [|7; 8; 9|]|];;
- : int vect vect = [|[|1; 2; 3|]; [|4; 5; 
6|]; [|7; 8; 9|]|]
#make_matrix 2 1 "Bonjour";;
- : string vect vect = [|[|"Bonjour"|]; 
[|"Bonjour"|]|]
#let M = make_matrix 2 3 0;;
M : int vect vect = [|[|0; 0; 0|]; [|0; 0; 
0|]|]
#let M2 = init_vect 3 (function i -> 
   init_vect 2 (function j -> i+j));;
M2 : int vect vect = [|[|0; 1|]; [|1; 2|]; 
[|2; 3|]|]
#(* nombre de lignes *)
 vect_length M;; 
- : int = 2
#(* nombre de colonnes *)
 vect_length M.(0);; 
- : int = 3

Consultation du contenu courant

#M;;
- : int vect vect = [|[|0; 0; 0|]; [|0; 0; 
0|]|]
#M.(0).(2);;
- : int = 0

Modification du contenu

#M.(1).(0) <- 2; M.(1).(2) <- 5;;
- : unit = ()
#M;;
- : int vect vect = [|[|0; 0; 0|]; [|2; 0; 
5|]|]

Séquences

#print_string "Bonjour "; 
 print_string "tout le monde !";;
Bonjour tout le monde !- : unit = ()
#print_string;;
- : string -> unit = <fun>
#1+2;3;;
Entrée interactive:
>1+2;3;;
>^^^
Attention: cette expression est de type 
int,
mais est utilisée avec le type unit.
- : int = 3

Boucles

Syntaxe:
while condition do actions done
for ident = début to findoactionsdone
for ident = début downto findoactionsdone

Exemples:

#for i = 0 to 9 do print_int i done;;
0123456789- : unit = ()
#let i = ref 0 in
 while !i <= 9 do
    print_int !i; incr i
 done;;
0123456789- : unit = ()
#for i = 9 downto 0 do print_int i done;;
9876543210- : unit = ()
#for i = 0 to (vect_length r)-1 do
   print_string r.(i); print_string " "
 done;;
Bonjour tout le monde! - : unit = ()

#for i = 0 to (vect_length M)-1 do
   for j = 0 to (vect_length M.(0))-1 do
   print_int M.(i).(j); print_string " "
   done;
   print_newline ()
 done;;
0 0 0 
2 0 5 
- : unit = ()

Exceptions (non détaillé en cours)

Réponse propre quand il n'y a pas de réponse pertinente
failwith déjà vu
Des exceptions nommées (plus précis pour récupérer, etc.)
Un mécanisme de traitement d'exceptions doit permettre de réaliser trois actions :
- déclarer une exception (si elle n'est pas prédéfinie);
- déclencher, lever, ou signaler une exception;
- traiter l'exception.

Les exceptions prédéfinies

exception Division_by_zero
exception Out_of_memory
exception Invalid_argument of string
exception Failure of string
exception Not_found

Deux levées d'exceptions prédéfinies

value failwith : string -> 'a
value invalid_arg : string -> 'a

Exemples de levée des exceptions prédéfinies

#(* Par des opérations prédéfinies *)
 1/0;;
Exception non rattrapée: Division_by_zero
#hd [];;
Exception non rattrapée: Failure "hd"
#[|1;2;3|].(10);;
Exception non rattrapée: Invalid_argument 
"vect_item"
#(* Par des fonctions que l'on définit *)
 let rec member = 
   function nom -> function liste -> 
 match liste with
 | [] -> raise Not_found
 | e::l -> e=nom || member nom l;;  
member : 'a -> 'a list -> bool = <fun>
#member 1 [1;2;3];;
- : bool = true
#member 4 [1;2;3];;
Exception non rattrapée: Not_found
#let chiffre1 = function n ->
   if n < 10 then n else 
   raise (Invalid_argument (string_of_int n));;
chiffre1 : int -> int = <fun>
#chiffre1 12;;
Exception non rattrapée: Invalid_argument 
"12"
#let chiffre2 = function n ->
   if n < 10 then n else 
   invalid_arg (string_of_int n);;
chiffre2 : int -> int = <fun>
#chiffre2 12;;
Exception non rattrapée: Invalid_argument 
"12"
#let chiffre3 = function n ->
   if n < 10 then n else 
   failwith "chiffre3: argument > 10";;
chiffre3 : int -> int = <fun>

#chiffre3 12;;
Exception non rattrapée: Failure 
"chiffre3: argument > 10"
#let chiffre4 = function n ->
   if n < 10 then n else 
   raise (Failure "chiffre4: argument > 10");;
chiffre4 : int -> int = <fun>
#chiffre4 12;;
Exception non rattrapée: Failure 
"chiffre4: argument > 10"

Déclaration (exception) et type (exn, type somme prédéfini extensible)

#(* Sans argument *)
 exception Stop;;
L'exception Stop est définie.
#Stop;;
- : exn = Stop
#(* Avec argument *)
 exception Trouvé of int;;
L'exception Trouvé est définie.
#Trouvé;;
- : int -> exn = <fun>
#Match_failure;;
- : string * int * int -> exn = <fun>

Levée (raise)
```
... 
raise exception 
...
```

Exemples de levées d'exceptions définies

#let search = function e -> function v ->
   for i = 0 to vect_length v - 1 do
     if v.(i)=e then raise (Trouvé i)
   done;;
search : 'a -> 'a vect -> unit = <fun>
#let search = function e -> function v ->
   let i = ref 0 in
   while true do 
     if v.(!i)=e then raise (Trouvé !i);
     i := !i+1
   done;;
search : 'a -> 'a vect -> unit = <fun>
#search "B" [|"A";"B";"C";"D"|];;
Exception non rattrapée: Trouvé 1
#search "E" [|"A";"B";"C";"D"|];;
Exception non rattrapée: Invalid_argument 
"vect_item"
#let failwith s = raise (Failure s);;
failwith : string -> 'a = <fun>

Une levée d'exception est un effet de bord.

Rattrapage ou récupération (try ... with)

try expression with 
| exception_1 -> expression_1
| exception_2 -> expression_2
| :
| exception_n -> expression_n

On appelle l'expression try ... with le traite-exception de l'exception exception_j.

Chaque expression_i peut lever à nouveau une des exceptions exception_j.

#(* Sous-vecteur d'un vecteur v commençant 
    à la première occurrence de l'élément e
    dans v *)
 let sous_vecteur = 
   function e -> function v ->
 try search e v;[|"impossible"|] with
 | Trouvé i -> 
   sub_vect v i (vect_length v - i)
 | Invalid_argument "vect_item" -> [||];;
sous_vecteur : string -> string vect -> 
string vect = <fun>
#sous_vecteur "B" [|"A";"B";"C";"D"|];;
- : string vect = [|"B"; "C"; "D"|]
#sous_vecteur "E" [|"A";"B";"C";"D"|];;
- : string vect = [||]
#let sans_doublons = function v -> 
   try 
     for i = 0 to vect_length v - 1 do
       if v.(i)=v.(i+1) then raise Stop
     done; true 
   with Stop -> false;;
sans_doublons : 'a vect -> bool = <fun>

#exception absent of int;;
L'exception absent est définie.
#let rec trouve_nom = 
   function numéro -> function amphi ->
 match amphi with
 | [] -> raise (absent numéro)
 | (x,n)::reste -> 
   if n=numéro then x 
   else trouve_nom numéro reste;;
trouve_nom : int -> ('a * int) list -> 'a 
= <fun>
#let verif = function (numéro, amphi) ->
   try (trouve_nom numéro amphi) with
   | absent p -> "chercher_à_la_scolarité";;
verif : int * (string * int) list -> 
string = <fun>

#exception erreur of int;;
L'exception erreur est définie.
#exception signal of string;;
L'exception signal est définie.
#let f_qui_déclenche = function x ->
   if x < 0 then raise (erreur (-x)) else 
   if x=0 
      then raise (signal "reprise au vol") 
   else x;; 
f_qui_déclenche : int -> int = <fun>
#f_qui_déclenche (-4);;
Exception non rattrapée: erreur 4
#f_qui_déclenche 2;;
- : int = 2
#let récupère = function x ->
   try f_qui_déclenche x with
   | erreur 0 -> 0 
   | erreur y -> 25-y+3*x 
   | signal _ -> 100*x+1;;
récupère : int -> int = <fun>
#(récupère 2),(récupère (-4)),(récupère 0);;
- : int * int * int = 2, 9, 1

Les exceptions comme style de programmation

à la place de sentinelles, permet notamment d'interrompre des boucles parcourant toute une structure dès que l'on a trouvé dans la structure un élément vérifiant une propriété donnée

#let sans_doublons = function v ->
   let i = ref 0 
   and t = ref false in
   while !i < vect_length v && not !t do
     if v.(!i)=v.(!i+1) then t := true;
     i := !i+1
   done; !t;;
sans_doublons : 'a vect -> bool = <fun>
#let rec member_rec = 
   function e -> function l -> 
 match l with
 | [] -> raise Not_found
 | e'::l' -> 
   if e=e' then raise Stop 
   else member_rec e l';;
member_rec : 'a -> 'a list -> 'b = <fun>
#let member = function e -> function l -> 
   try member_rec e l with
   | Not_found -> false
   | Stop -> true;;
member : 'a -> 'a list -> bool = <fun>
#member 2 [1;2;3];;
- : bool = true
#member 4 [1;2;3];;
- : bool = false
#let rec member e l = 
   try e = hd l or member e (tl l)  
   with Failure "hd" -> false;;
member : 'a -> 'a list -> bool = <fun>
#member 2 [1;2;3];;
- : bool = true
#member 4 [1;2;3];;
- : bool = false

Programmation fonctionnelle vs impérative

Utiliser ce qui paraît le plus simple, le plus naturel.
Même si votre expérience est surtout impérative, ne pas oublier que le style fonctionnel est souvent plus compact ou plus facile à comprendre.

Exemples dans les deux styles

#let rec fact = function n ->
   if n <= 0 then 1 else n*fact(n-1);;
fact : int -> int = <fun>
#let fact_imp = function n ->
   let temp = ref 1 in
     for i = 1 to n do
       temp :=!temp*i
     done;
   !temp ;;
fact_imp : int -> int = <fun>
#let rec fib1 = function n ->
   if n <= 1 then 1 
   else fib1(n-1)+fib1(n-2);;
fib1 : int -> int = <fun>

#let fib2 = function n ->
   let (cour, prec, temp) = 
       (ref 1, ref 1, ref 1) in
     for i = 1 to n-1 do
       temp := !cour;
       cour := !cour + !prec;
       prec := !temp
     done; !cour;;
fib2 : int -> int = <fun>
#let fib3 = function p ->
   let rec fib_accu = function prec -> 
     function cour -> function n ->
       if p = n then cour
       else fib_accu cour (prec+cour) (n+1) in
   if p <= 1 then 1 else fib_accu 1 1 1;;
fib3 : int -> int = <fun>

Partie: II
Un exemple complet
complément sur les types polymorphes (non détaillé en cours)

Types

#type 'a arbre = Vide | Noeud of 'a * 'a arbre * 'a arbre;;
Le type arbre est défini.

ou bien

#type 'a arbre = Vide | Noeud of 'a arbre_non_vide
 and 'a arbre_non_vide = 
   { Étiquette: 'a; 
     Fils_gauche: 'a arbre; 
     Fils_droit: 'a arbre };;
Le type arbre est défini.
Le type arbre_non_vide est défini.

ou encore

#type ('a, 'b) arbre = 
 | Vide | Feuille of 'b | Noeud of ('a, 'b) arbre_non_vide
 and ('a, 'b) arbre_non_vide = 
   { Étiquette: 'a; 
     Fils_gauche: ('a, 'b) arbre; 
     Fils_droit: ('a, 'b) arbre };;
Le type arbre est défini.
Le type arbre_non_vide est défini.

Exemples

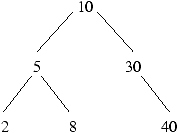
Figure 0.2 : mon_arbre

#let mon_arbre = Noeud 
   {Étiquette = 10;
    Fils_gauche = Noeud 
      {Étiquette = 5; 
       Fils_gauche = Feuille 2; Fils_droit = Feuille 8}; 
    Fils_droit = Noeud 
      {Étiquette = 30; 
       Fils_gauche = Vide; Fils_droit = Feuille 40}};;
mon_arbre : (int, int) arbre = Noeud ...

#let mon_arbre = Noeud 
   {Étiquette = 10;
    Fils_gauche = Noeud 
      {Étiquette = 5; 
       Fils_gauche = Noeud 
         {Étiquette = 2; 
          Fils_gauche = Vide; Fils_droit = Vide};
       Fils_droit = Noeud 
         {Étiquette = 8; 
          Fils_gauche = Vide; Fils_droit = Vide}}; 
    Fils_droit = Noeud 
      {Étiquette = 30; 
       Fils_gauche = Vide; 
       Fils_droit = Noeud 
         {Étiquette = 40; 
          Fils_gauche = Vide; Fils_droit = Vide}}};;
mon_arbre : (int, 'a) arbre = Noeud ...

Figure 0.3 : mon_expr

#type op = 
 | Addition | Soustraction | Multiplication | Division;;
Le type op est défini.

#let mon_expr = Noeud
   {Étiquette = Addition; 
    Fils_gauche = Noeud
      {Étiquette = Multiplication; 
       Fils_gauche = Feuille 1; Fils_droit = Feuille 2};
    Fils_droit = Noeud
      {Étiquette = Soustraction; 
       Fils_gauche = Feuille 3;
       Fils_droit = Noeud 
         {Étiquette = Division; 
          Fils_gauche = Feuille 4; Fils_droit = Feuille 5}}};;
mon_expr : (op, int) arbre = Noeud ...

Imprimer l'arbre par un parcours infixe

#let rec print_arbre print_étiquette print_feuille arbre = 
 match arbre with
 | Vide -> ()
 | Feuille f -> print_feuille f
 | Noeud {Étiquette = e;Fils_gauche = fg;Fils_droit = fd} ->
     print_string "(";
     print_arbre print_étiquette print_feuille fg;
     print_étiquette e; 
     print_arbre print_étiquette print_feuille fd;
     print_string ")";;
print_arbre : ('a -> 'b) -> ('c -> unit) -> ('a, 'c) arbre 
-> unit = <fun>
#print_arbre print_int print_int mon_arbre;;
(((2)5(8))10(30(40)))- : unit = ()

#let print_op op = match op with
 | Addition -> print_string "+"
 | Soustraction -> print_string "-"
 | Multiplication -> print_string "*"
 | Division -> print_string "/";;
print_op : op -> unit = <fun>
#print_arbre print_op print_int mon_expr;;
((1*2)+(3-(4/5)))- : unit = ()

Trier une liste en utilisant un arbre binaire de recherche

#let rec insérer_arbre x arbre = match arbre with
 | Vide -> Feuille x
 | Feuille y -> 
     if x < y 
     then Noeud {Étiquette = y; Fils_gauche = Feuille x; 
                 Fils_droit = Vide} 
     else Noeud {Étiquette = y; Fils_gauche = Vide; 
                 Fils_droit = Feuille x}
 | Noeud {Étiquette = e;Fils_gauche = fg;Fils_droit = fd} ->  
     if x < e 
     then Noeud {Étiquette = e; 
                 Fils_gauche = insérer_arbre x fg; 
                 Fils_droit = fd}
     else Noeud {Étiquette = e; Fils_gauche = fg; 
                 Fils_droit = insérer_arbre x fd};;
insérer_arbre : 'a -> ('a, 'a) arbre -> ('a, 'a) arbre = 
<fun>
#let rec arbre_of_list l = match l with 
 | [] -> Vide
 | x::l' -> insérer_arbre x (arbre_of_list l');;
arbre_of_list : 'a list -> ('a, 'a) arbre = <fun>
#print_arbre print_int print_int 
   (arbre_of_list [ 2; 5; 4; 6; 3; 7; 1; 8; 0; 5 ]);;
((0(1(234)))5(((56)7)8))- : unit = ()
#let rec list_of_arbre arbre = match arbre with
 | Vide -> []
 | Feuille f -> [f]
 | Noeud {Étiquette = e;Fils_gauche = fg;Fils_droit = fd} ->
     (list_of_arbre fg)@[e]@(list_of_arbre fd);;
list_of_arbre : ('a, 'a) arbre -> 'a list = <fun>
#let tri l = list_of_arbre (arbre_of_list l);;
tri : 'a list -> 'a list = <fun>
#tri [ 2; 5; 4; 6; 3; 7; 1; 8; 0; 5 ];;
- : int list = [0; 1; 2; 3; 4; 5; 5; 6; 7; 8]

et maintenant en tenant compte d'une fonction d'ordre totale

#let rec insérer_arbre ordre x arbre = match arbre with
 | Vide -> Feuille x
 | Feuille y -> 
     if ordre x y 
     then Noeud {Étiquette = y; Fils_gauche = Feuille x; 
                 Fils_droit = Vide } 
     else Noeud {Étiquette = y; Fils_gauche = Vide; 
                 Fils_droit = Feuille x }
 | Noeud {Étiquette = e;Fils_gauche = fg;Fils_droit = fd} ->  
     if ordre x e 
     then Noeud {Étiquette = e; 
                 Fils_gauche = insérer_arbre ordre x fg; 
                 Fils_droit = fd}
     else Noeud {Étiquette = e; Fils_gauche = fg; 
                 Fils_droit = insérer_arbre ordre x fd};;
insérer_arbre :
 ('a -> 'a -> bool) -> 'a -> ('a, 'a) arbre -> ('a, 'a) 
arbre = <fun>

#let rec arbre_of_list ordre l = match l with 
 | [] -> Vide
 | x::l' -> insérer_arbre ordre x (arbre_of_list ordre l');;
arbre_of_list : ('a -> 'a -> bool) -> 'a list -> ('a, 'a) 
arbre = <fun>
#let rec list_of_arbre arbre = match arbre with
 | Vide -> []
 | Feuille f -> [f]
 | Noeud a ->
     (list_of_arbre a.Fils_gauche)@
     [a.Étiquette]@
     (list_of_arbre a.Fils_droit);;
list_of_arbre : ('a, 'a) arbre -> 'a list = <fun>
#let tri ordre l = list_of_arbre (arbre_of_list ordre l);;
tri : ('a -> 'a -> bool) -> 'a list -> 'a list = <fun>
#tri (prefix <) [ 2; 5; 4; 6; 3; 7; 1; 8; 0; 5 ];;
- : int list = [0; 1; 2; 3; 4; 5; 5; 6; 7; 8]
#tri (prefix >) [ 2; 5; 4; 6; 3; 7; 1; 8; 0; 5 ];;
- : int list = [8; 7; 6; 5; 5; 4; 3; 2; 1; 0]

Évaluation d'un arbre d'expression

#let rec évaluation arbre = match arbre with
 | Vide -> 0
 | Feuille i -> i
 | Noeud a ->
     let efg = évaluation a.Fils_gauche 
     and efd = évaluation a.Fils_droit in
     match a.Étiquette with 
     | Addition -> efg + efd
     | Soustraction -> efg - efd
     | Multiplication -> efg * efd
     | Division -> efg / efd;;
évaluation : (op, int) arbre -> int = <fun>
#évaluation mon_expr;;
- : int = 5

Expressions avec variables

#type constructeur = 
 | Variable | Constante | Plus | Multiplié;;
Le type constructeur est défini.
#let mon_exp = Noeud 
   {Étiquette = Plus; 
    Fils_gauche = Noeud 
      {Étiquette = Variable;
       Fils_gauche = Feuille 1; Fils_droit = Vide}; 
    Fils_droit = Noeud 
      {Étiquette = Plus; 
       Fils_gauche = Noeud 
         {Étiquette = Variable; Fils_gauche = Feuille 1;
          Fils_droit = Vide}; 
       Fils_droit = Noeud 
         {Étiquette = Constante; Fils_gauche = Feuille 3;
          Fils_droit = Vide}}};;
mon_exp : (constructeur, int) arbre = Noeud ...

Ce document a été traduit de L^AT_EX par H^EV^EA.